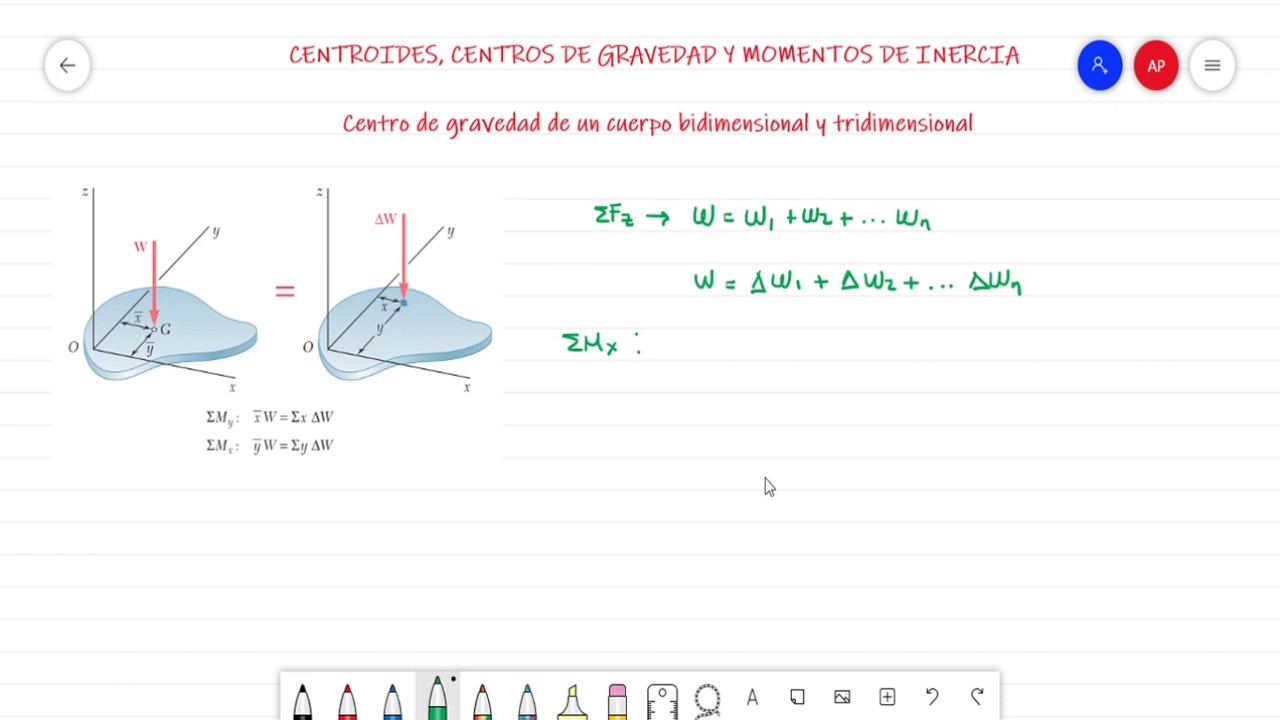
¿Alguna vez te has preguntado cómo se determina el equilibrio de un objeto? El centro de gravedad es el punto donde se puede considerar que toda la masa de un cuerpo está concentrada. Para los cuerpos bidimensionales, como figuras planas, calcular este punto puede parecer complicado, pero no te preocupes, ¡estás en el lugar correcto! En este artículo, vamos a desglosar el proceso en pasos sencillos que podrás seguir fácilmente. Así que, si te interesa saber más sobre este concepto fundamental en física y matemáticas, sigue leyendo.
¿Qué es el Centro de Gravedad?
El centro de gravedad es un concepto crucial en física que se refiere al punto en el que se equilibra un objeto. Imagina que estás sosteniendo un lápiz en el aire. Si lo sostienes en su centro, el lápiz no se caerá. Esto es porque el centro de gravedad se encuentra justo ahí. Pero, ¿qué pasa si el lápiz es más largo o tiene un extremo más pesado? En este caso, el centro de gravedad se desplaza. En un cuerpo bidimensional, como un triángulo o un cuadrado, el centro de gravedad puede calcularse utilizando algunas fórmulas matemáticas.
¿Por Qué es Importante el Centro de Gravedad?
Entender el centro de gravedad es vital en diversas disciplinas. En ingeniería, por ejemplo, es esencial para diseñar estructuras estables. En el deporte, los atletas deben conocer su propio centro de gravedad para mejorar su rendimiento. Además, en la vida cotidiana, este conocimiento puede ayudarte a equilibrar objetos de manera más eficiente. Así que, ya sea que estés construyendo una casa, practicando un deporte o simplemente tratando de apilar cajas, el centro de gravedad juega un papel crucial.
Pasos para Calcular el Centro de Gravedad de un Cuerpo Bidimensional
Ahora que entendemos qué es y por qué es importante, pasemos a la parte divertida: ¡calcularlo! Vamos a desglosar el proceso en pasos simples.
Paso 1: Identificar la Forma del Cuerpo
El primer paso es identificar la forma del cuerpo bidimensional. ¿Es un triángulo, un cuadrado, un círculo o una figura más compleja? Cada forma tiene su propio método de cálculo. Por ejemplo, el centro de gravedad de un triángulo se encuentra en el punto de intersección de sus medianas, mientras que el de un cuadrado está en su centro.
Paso 2: Dividir en Figuras Simples
Si la figura es complicada, intenta dividirla en formas más simples. Por ejemplo, si tienes una figura en forma de L, puedes dividirla en un rectángulo y un cuadrado. Esto facilita el cálculo del centro de gravedad de cada sección por separado.
Paso 3: Calcular el Centro de Gravedad de Cada Parte
Una vez que tengas tus formas simples, calcula el centro de gravedad de cada una. Aquí hay algunas fórmulas rápidas:
– Rectángulo: El centro de gravedad está en el punto medio, así que simplemente toma la mitad de la longitud y la mitad del ancho.
– Triángulo: El centro de gravedad se encuentra a 1/3 de la altura desde la base y en el punto medio de la base.
– Círculo: El centro de gravedad está en el centro del círculo.
Paso 4: Calcular el Área de Cada Parte
Después de encontrar el centro de gravedad de cada figura, necesitarás calcular el área de cada una. Esto es importante porque el centro de gravedad total dependerá del área de cada parte. Las fórmulas para el área son las siguientes:
– Rectángulo: Área = base × altura
– Triángulo: Área = (base × altura) / 2
– Círculo: Área = π × radio²
Paso 5: Usar la Fórmula del Centro de Gravedad
Ahora que tienes el centro de gravedad y el área de cada figura, es hora de calcular el centro de gravedad total de la figura compuesta. La fórmula es la siguiente:
[
bar{x} = frac{sum (x_i cdot A_i)}{sum A_i}
]
[
bar{y} = frac{sum (y_i cdot A_i)}{sum A_i}
]
Donde ( bar{x} ) y ( bar{y} ) son las coordenadas del centro de gravedad total, ( x_i ) y ( y_i ) son las coordenadas del centro de gravedad de cada parte, y ( A_i ) es el área de cada parte.
Paso 6: Interpretar los Resultados
Una vez que hayas hecho los cálculos, interpreta los resultados. ¿El centro de gravedad se encuentra dentro de la figura? Si es así, ¡genial! Eso significa que la figura está equilibrada. Si está fuera, podría ser un problema de estabilidad.
Ejemplo Práctico
Para que todo esto sea más claro, hagamos un ejemplo práctico. Supongamos que tienes un rectángulo de 4 cm de largo y 2 cm de ancho, y un triángulo con una base de 4 cm y una altura de 3 cm. Primero, calculamos el área y el centro de gravedad de cada figura.
– Rectángulo:
– Área = 4 cm × 2 cm = 8 cm²
– Centro de gravedad: (2 cm, 1 cm)
– Triángulo:
– Área = (4 cm × 3 cm) / 2 = 6 cm²
– Centro de gravedad: (2 cm, 1 cm)
Ahora, usamos la fórmula del centro de gravedad total:
[
bar{x} = frac{(2 cdot 8) + (2 cdot 6)}{8 + 6} = frac{16 + 12}{14} = 2 cm
]
[
bar{y} = frac{(1 cdot 8) + (1 cdot 6)}{8 + 6} = frac{8 + 6}{14} = 1 cm
]
Por lo tanto, el centro de gravedad total de la figura compuesta está en (2 cm, 1 cm).
Consejos Útiles
– Siempre verifica tus cálculos. Un pequeño error puede llevar a un resultado incorrecto.
– Si te resulta difícil visualizar las formas, dibuja un boceto. A veces, ver las cosas gráficamente puede ayudarte a comprender mejor el problema.
– Practica con diferentes formas. Cuanto más practiques, más cómodo te sentirás con el proceso.
Calcular el centro de gravedad de un cuerpo bidimensional no tiene por qué ser un proceso intimidante. Siguiendo estos pasos y utilizando las fórmulas adecuadas, puedes descomponer cualquier figura en partes manejables y encontrar su centro de gravedad con facilidad. Ya sea que estés en la escuela, trabajando en un proyecto de ingeniería o simplemente tengas curiosidad, este conocimiento puede ser increíblemente útil.
¿El centro de gravedad siempre está dentro del objeto?
No necesariamente. En algunas figuras irregulares, el centro de gravedad puede estar fuera del objeto, lo que podría afectar su estabilidad.
¿Cómo afecta el centro de gravedad al equilibrio de un objeto?
Un objeto es más estable cuando su centro de gravedad está bajo y centrado. Si el centro de gravedad se desplaza demasiado hacia un lado, el objeto puede volcarse.
¿Se puede calcular el centro de gravedad de figuras tridimensionales de la misma manera?
La idea es similar, pero las fórmulas y métodos de cálculo son más complejos. Para cuerpos tridimensionales, se utilizan integrales en muchos casos.
¿Es necesario tener en cuenta el peso de los materiales en el cálculo del centro de gravedad?
Sí, si los materiales tienen diferentes densidades, esto puede afectar la ubicación del centro de gravedad y debería ser considerado en los cálculos.
¿El centro de gravedad cambia si la figura se deforma?
Sí, cualquier cambio en la forma o en la distribución de masa de un objeto puede cambiar su centro de gravedad. Por eso es importante recalcularlo si se realizan modificaciones significativas.
¡Espero que esta guía te haya sido útil! ¿Tienes más preguntas sobre el centro de gravedad? ¡No dudes en preguntar!