¿Alguna vez te has preguntado cómo se comportan los objetos al moverse? ¿Por qué algunos se equilibran fácilmente mientras que otros parecen tambalearse? Todo esto se relaciona con un concepto fundamental en física: el centro de masa. En este artículo, vamos a explorar cómo hallar el centro de masa de diferentes objetos de una manera sencilla y práctica. Te prometo que no será un viaje aburrido; al contrario, lo haremos interesante y fácil de entender. Así que, ¡prepárate para sumergirte en el fascinante mundo de la física!
### ¿Qué es el Centro de Masa?
Primero, aclaremos qué es exactamente el centro de masa. Imagina que tienes un objeto irregular, como una figura de arcilla. Si lo sostienes en un punto, ese punto es donde la figura puede equilibrarse. Eso es el centro de masa. Es el punto donde se concentra la masa del objeto y, en un sentido práctico, es el «equilibrio» del mismo. En un objeto simétrico, como una esfera o un cubo, el centro de masa está en el centro geométrico. Pero cuando hablamos de formas irregulares, las cosas se complican un poco.
### ¿Por qué es Importante Conocer el Centro de Masa?
Entender el centro de masa es crucial en muchos campos, desde la ingeniería hasta la biología. Por ejemplo, los ingenieros utilizan este concepto para diseñar vehículos que sean seguros y estables. Los arquitectos lo aplican para crear edificios que puedan resistir fuerzas externas, como vientos fuertes o terremotos. Y, si alguna vez has jugado a equilibrar un lápiz en la punta de tu dedo, sabes que el centro de masa juega un papel clave en el equilibrio.
### Cómo Hallar el Centro de Masa: Un Enfoque Paso a Paso
Ahora que tenemos una idea clara de qué es el centro de masa y por qué es importante, vamos a entrar en materia. Aquí te presento un enfoque paso a paso para hallar el centro de masa de un objeto:
#### Paso 1: Identifica el Objeto
El primer paso es identificar el objeto del que deseas hallar el centro de masa. Puede ser un objeto simple, como una barra de madera, o algo más complejo, como un sistema de partículas. La complejidad del objeto determinará el método que usarás.
#### Paso 2: Divide el Objeto en Partes
Si el objeto es irregular, una buena estrategia es dividirlo en partes más simples. Por ejemplo, si tienes un objeto en forma de «L», puedes dividirlo en un rectángulo y un cuadrado. Esto te facilitará el cálculo.
#### Paso 3: Encuentra el Centro de Masa de Cada Parte
Para cada parte del objeto, calcula el centro de masa. Si trabajas con formas geométricas simples, como un cuadrado o un triángulo, el centro de masa se encuentra fácilmente. Por ejemplo, el centro de masa de un triángulo se encuentra en el punto donde se cruzan las medianas.
#### Paso 4: Asigna un Sistema de Coordenadas
Para facilitar los cálculos, asigna un sistema de coordenadas. Puedes usar coordenadas cartesianas (x, y) donde el origen (0, 0) puede ser una esquina del objeto. Esto te ayudará a localizar cada centro de masa en un plano.
#### Paso 5: Calcula la Masa de Cada Parte
Ahora que tienes los centros de masa, necesitas conocer la masa de cada parte. Si no conoces la masa, tendrás que medirla. Esto es importante porque el centro de masa del objeto total dependerá de la masa de cada parte.
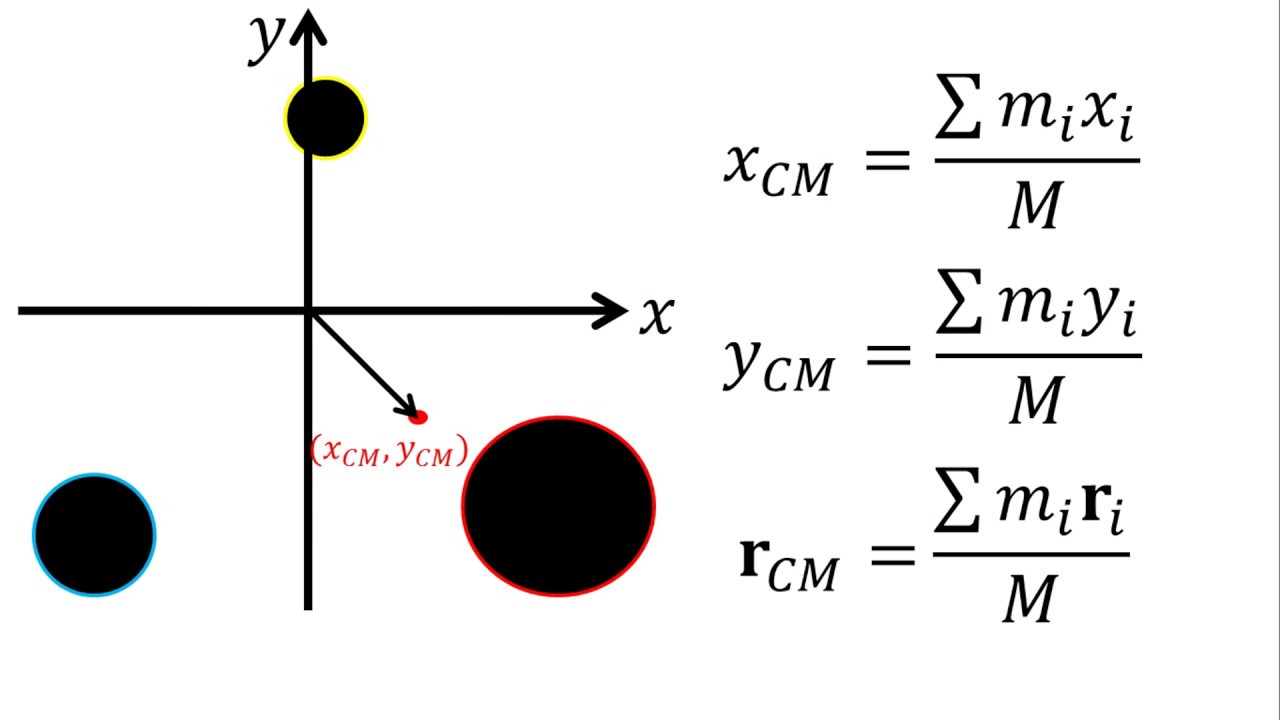
#### Paso 6: Aplica la Fórmula del Centro de Masa
La fórmula general para hallar el centro de masa (C) de un sistema de partículas es:
[
C = frac{sum (m_i cdot r_i)}{sum m_i}
]
donde (m_i) es la masa de cada parte y (r_i) es la posición del centro de masa de cada parte.
#### Paso 7: Suma y Simplifica
Finalmente, suma todos los productos de masa y posición, y luego divide por la masa total. Esto te dará la posición del centro de masa del objeto completo.
### Ejemplo Práctico: Hallando el Centro de Masa de una Barra de Madera
Imagina que tienes una barra de madera de 2 metros de largo, con una masa de 4 kg. Para simplificar, supongamos que la barra es homogénea, lo que significa que su masa está distribuida uniformemente.
1. Identificación: Una barra de 2 m y 4 kg.
2. División: No es necesario dividirla, ya que es un objeto simple.
3. Centro de Masa de la Parte: El centro de masa de una barra uniforme está en su centro, es decir, a 1 metro.
4. Sistema de Coordenadas: Asignamos el extremo izquierdo como (0, 0).
5. Masa: La masa total es de 4 kg.
6. Aplicación de la Fórmula: Usamos la fórmula del centro de masa:
[
C = frac{(4 , text{kg} cdot 1 , text{m})}{4 , text{kg}} = 1 , text{m}
]
7. Resultado: El centro de masa de la barra de madera está a 1 metro del extremo izquierdo.
### Ejemplo Adicional: Hallando el Centro de Masa de un Sistema de Partículas
Ahora, supongamos que tenemos un sistema de tres partículas con las siguientes masas y posiciones:
– Partícula 1: (m_1 = 2 , text{kg}), (r_1 = (1, 2))
– Partícula 2: (m_2 = 3 , text{kg}), (r_2 = (4, 0))
– Partícula 3: (m_3 = 5 , text{kg}), (r_3 = (0, 3))
Siguiendo el mismo procedimiento:
1. Identificación: Tres partículas con diferentes masas y posiciones.
2. División: No es necesario dividir, ya que son partículas.
3. Centro de Masa: Calculamos el centro de masa utilizando la fórmula:
[
C_x = frac{(m_1 cdot x_1 + m_2 cdot x_2 + m_3 cdot x_3)}{(m_1 + m_2 + m_3)}
]
[
C_y = frac{(m_1 cdot y_1 + m_2 cdot y_2 + m_3 cdot y_3)}{(m_1 + m_2 + m_3)}
]
Calculando:
[
C_x = frac{(2 cdot 1 + 3 cdot 4 + 5 cdot 0)}{(2 + 3 + 5)} = frac{(2 + 12 + 0)}{10} = frac{14}{10} = 1.4
]
[
C_y = frac{(2 cdot 2 + 3 cdot 0 + 5 cdot 3)}{(2 + 3 + 5)} = frac{(4 + 0 + 15)}{10} = frac{19}{10} = 1.9
]
El centro de masa del sistema de partículas está en (C = (1.4, 1.9)).
### Conclusión
Y ahí lo tienes, un recorrido completo sobre cómo hallar el centro de masa de diferentes objetos. Desde entender su significado hasta aplicar fórmulas, hemos cubierto todos los aspectos esenciales. Así que, la próxima vez que te enfrentes a un objeto irregular o un sistema de partículas, ya sabes qué hacer.
### Preguntas Frecuentes
1. ¿El centro de masa siempre está dentro del objeto?
No necesariamente. En algunos casos, como en un objeto con forma de «C», el centro de masa puede estar fuera del objeto.
2. ¿Cómo afecta la forma del objeto al centro de masa?
La forma del objeto influye en la distribución de la masa, lo que a su vez afecta la ubicación del centro de masa.
3. ¿Es lo mismo el centro de masa que el centro geométrico?
No, aunque en objetos simétricos son iguales, en objetos irregulares pueden diferir.
4. ¿Qué pasa si el objeto está en movimiento?
El centro de masa en movimiento sigue siendo el mismo, pero su posición cambiará con el tiempo según la trayectoria del objeto.
5. ¿Se puede calcular el centro de masa en 3D?
Sí, el concepto de centro de masa se puede extender a tres dimensiones utilizando coordenadas (x, y, z) y aplicando fórmulas similares.
Espero que este artículo te haya ayudado a entender mejor el concepto de centro de masa y cómo calcularlo. ¡Hasta la próxima!