¿Alguna vez te has preguntado cómo se determina el punto en el que se equilibra un objeto? Esa es la esencia del centro de masa, un concepto fundamental en la física que nos ayuda a entender cómo se comportan los cuerpos en movimiento. Imagina que estás jugando con un péndulo; el punto en el que cuelga en equilibrio es, en términos sencillos, su centro de masa. Pero, ¿cómo llegamos a calcularlo? En este artículo, vamos a desglosar el proceso de encontrar el centro de masa de manera sencilla y práctica, utilizando ejemplos que te harán sentir como un experto en la materia. Así que, ¡abróchate el cinturón y vamos a ello!
¿Qué es el Centro de Masa?
El centro de masa es el punto en un objeto o sistema de partículas donde se puede considerar que toda su masa está concentrada. En otras palabras, es el «promedio ponderado» de la posición de todas las partículas que componen un cuerpo. Pero no te preocupes, no necesitas ser un físico para entenderlo. Piensa en un columpio; si te sientas en un extremo, el columpio se inclina hacia ese lado. Si te mueves al centro, el columpio se equilibra. ¡Eso es el centro de masa en acción!
¿Por qué es Importante el Centro de Masa?
Conocer el centro de masa de un objeto es crucial en múltiples campos, desde la ingeniería hasta la biología. Por ejemplo, en la ingeniería, diseñar estructuras que puedan soportar cargas sin colapsar requiere un buen entendimiento de cómo se distribuye la masa. En deportes, los atletas utilizan su conocimiento sobre el centro de masa para mejorar su equilibrio y rendimiento. Además, en la vida cotidiana, incluso al cargar una mochila, tener en cuenta el centro de masa puede hacer una gran diferencia en la comodidad. Pero, ¿cómo podemos calcularlo? Aquí es donde entra nuestra guía paso a paso.
Paso 1: Identificar el Sistema
Lo primero que necesitas hacer es identificar el sistema que estás analizando. ¿Es un solo objeto, como una barra? ¿O es un conjunto de partículas, como un grupo de pelotas? Esto es fundamental porque el método que usarás para calcular el centro de masa dependerá de la complejidad del sistema. Para simplificar, empecemos con un objeto simple: una barra uniforme.
Paso 2: Determinar las Dimensiones y la Masa
Ahora que tienes tu objeto, el siguiente paso es medir sus dimensiones y conocer su masa. Supongamos que tienes una barra de 2 metros de longitud y 4 kilogramos de masa. Es importante ser preciso aquí, ya que cualquier error en las mediciones afectará el resultado final. En nuestro ejemplo, la longitud es 2 metros y la masa es 4 kg. Recuerda, ¡los detalles cuentan!
Paso 3: Usar la Fórmula del Centro de Masa
La fórmula básica para encontrar el centro de masa (CM) de un objeto uniforme es bastante simple: se encuentra en el punto medio del objeto. Así que, si nuestra barra mide 2 metros, el centro de masa se encuentra a 1 metro desde un extremo. ¡Fácil, ¿verdad?! Pero si el objeto no es uniforme, como una barra con diferentes densidades, entonces necesitarás usar una fórmula más compleja que involucra integrales. Pero no te preocupes, por ahora, mantendremos las cosas simples.
Paso 4: Aplicar el Método para Sistemas de Partículas
Si tienes un sistema de partículas, como un conjunto de bolas de diferentes masas, la fórmula se convierte en un poco más complicada. Aquí está la fórmula que puedes usar:
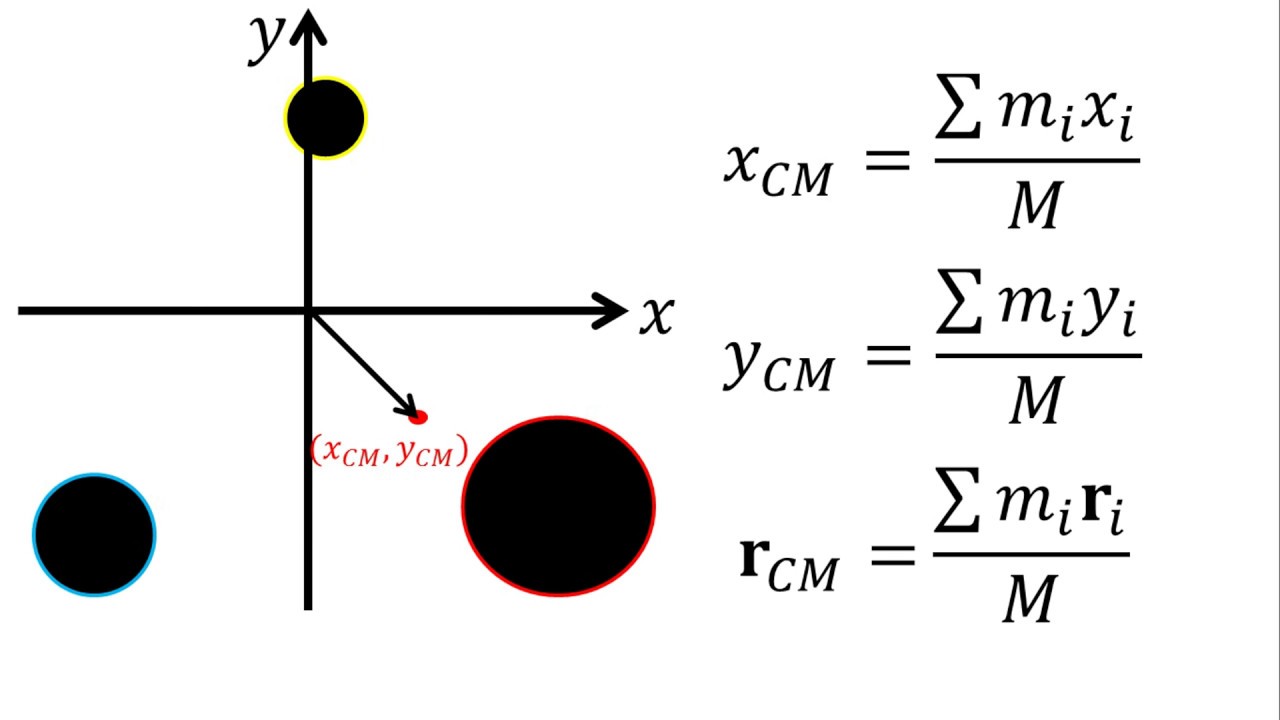
CM = (Σ(m_i * x_i)) / Σm_i
Donde m_i es la masa de cada partícula y x_i es la posición de cada partícula. Entonces, si tienes tres bolas de masa 1 kg, 2 kg y 3 kg ubicadas en 0, 1 y 2 metros respectivamente, el centro de masa se calcularía así:
- CM = [(1 kg * 0 m) + (2 kg * 1 m) + (3 kg * 2 m)] / (1 kg + 2 kg + 3 kg)
- CM = (0 + 2 + 6) / 6 = 1.33 metros
¡Y ahí lo tienes! El centro de masa de este sistema de partículas se encuentra a 1.33 metros del origen.
Paso 5: Verificar el Resultado
Una vez que hayas calculado el centro de masa, es fundamental que verifiques tu resultado. Puedes hacerlo visualizando el objeto o sistema en un modelo 3D o usando simulaciones en línea. También puedes intentar equilibrar el objeto en un punto y ver si se mantiene en equilibrio. Si no es así, es posible que necesites revisar tus cálculos. ¡La práctica hace al maestro!
Ejemplo Práctico: Calculando el Centro de Masa de un Triángulo
Ahora que hemos cubierto los pasos básicos, probemos con un ejemplo más complejo: calcular el centro de masa de un triángulo. Supongamos que tenemos un triángulo isósceles con una base de 4 metros y una altura de 3 metros. Para un triángulo, el centro de masa se encuentra en un punto específico: a un tercio de la altura desde la base.
Entonces, el centro de masa en este caso estaría a:
- CM = (1/3) * altura = (1/3) * 3 m = 1 m
Esto significa que el centro de masa del triángulo se encuentra a 1 metro sobre la base. ¡Eso no fue tan difícil, verdad?
Calcular el centro de masa puede parecer complicado al principio, pero una vez que entiendes los conceptos básicos, se convierte en un proceso relativamente sencillo. Ya sea que estés lidiando con un objeto simple o un sistema de partículas más complejo, seguir estos pasos te permitirá encontrar el centro de masa con facilidad. Recuerda, la práctica es clave, así que no dudes en experimentar con diferentes formas y sistemas para reforzar tu comprensión.
- ¿Puedo calcular el centro de masa de un objeto irregular? Sí, aunque es más complicado, puedes usar métodos de integración o aproximaciones mediante formas simples.
- ¿El centro de masa siempre está dentro del objeto? No necesariamente. En objetos con formas extrañas, el centro de masa puede estar fuera del objeto, como en un anillo.
- ¿Por qué es importante en la ingeniería? Conocer el centro de masa es esencial para diseñar estructuras que sean estables y seguras.
- ¿Hay herramientas para ayudar en el cálculo? Sí, existen software y aplicaciones que pueden facilitar estos cálculos, especialmente para formas complejas.